L'Hypothèse de Représentation Platonique dans un petit monde : le Morpion

Par Luc Pommeret

Introduction

Les LLMs sont des modèles dont la performance sur le langage humain n'est plus à démontrer. Fondée sur l'architecture transformer, leurs capacités hors-norme semblent parfois nous échapper, si bien qu'on ne comprend pas toujours comment le modèle infère ce qu'il infère.

Une hypothèse en particulier a attiré notre attention, parce qu'elle semble faire la synthèse de nombreuses observations éparses que l'on a pu faire dans le domaine de l'interprétabilité (ou explicabilité). Il s'agit de la PRH, ou Platonic Representation Hypothesis, qui postule que les modèles de transformer se forgent un modèle de représentation du monde durant l'entraînement, résultant de la recherche de simplicité que recherche naturellement un réseau de neurones qui apprend.

La conséquence la plus surprenante de leur hypothèse est que des modèles entraînés sur différents types de données (images, texte, sons, etc.) vont converger vers la même représentation dans leur espace latent. Notre but ici sera d'étudier en profondeur un cas simple, très simple, celui du Morpion. Dans ce jeu, dont l'ensemble des parties peut être généré en quelques minutes par un ordinateur moderne, le monde est très simple, et ne nécessite pas une immense puissance de calcul, autre avantage dont nous pourrons tirer parti.

Ici nous allons étudier les représentations de deux transformers : l'un est entraîné sur des images du jeu, et l'autre sur des séquences de coups sous forme de texte.

L'hypothèse principale que nous voulons tester est en somme si les deux représentations d'une même partie de Morpion convergent.

Pour préparer le terrain et explorer d'autres aspects de l'interprétation de l'architecture transformer, nous allons effectuer des tests à l'aide d'autres techniques, à commencer par le sondage (probing).

Comment représenter une partie de Morpion ?

Le morpion, comme les échecs ou les dames, est un jeu de plateau. Mais contrairement aux deux derniers, il est extrêmement simple, ce qui permet la complétude de l'analyse (on génère toutes les parties possibles, et on analyse notre transformer avec toutes ces parties).

Une manière très simple, voire enfantine, de représenter une partie de morpion est de la noter sous forme de dessin, côte à côte, en montrant l'état du plateau à chaque trait. C'est le format que nous avons choisi pour les images, qui ont donc une taille 9x9.

Pour noter les parties de Morpion textuellement, nous avons choisi de noter les coups les uns à la suite des autres, comme le format PGN aux échecs, ce qui donne un historique de la partie.

Le format du jeu de Morpion étant ce qu'il est, le nombre de coups ne peut excéder 9, ce qui est bien pratique pour la tokénisation, première étape de l'apprentissage.

Voici les tokénisations respectives des images et des textes (que l'on trouve dans les fichiers meta.pkl) :

{
"vocab_size": 4,
"itos": {"0": "b", "1": "n", "2": "g", "3": ";"},
"stoi": {"b": 0, "n": 1, "g": 2, ";": 3}
}
            

{
"vocab_size": 10,
"itos": {"0": ";", "1": " ", "2": "0", "3": "1", "4": "2", "5": "3", "6": "X", "7": "O", "8": "/", "9": "-"},
"stoi": {";": 0, " ": 1, "0": 2, "1": 3, "2": 4, "3": 5, "X": 6, "O": 7, "/": 8, "-": 9}
}
            

Les stoi et les itos ne sont pas grecs, mais un format de données qui permet de convertir les chaînes de caractères (strings) en entiers naturels (integers), c'est-à-dire string to integer ou plus simplement stoi, l'itos étant l'opération réciproque.

La tokénisation des images repose sur le pixel, qui sera blanc, valeur 0 (représenté par 'b'), si la case est saturée par un X, noire, valeur 1 (représenté par 'n'), si la case est saturée par un O, et grise, valeur 2 (représenté par 'g') si la case est vide. L'image est parcourue de manière naturelle, ligne par ligne pour former une ligne au format str (string).

Dans les deux cas, ";" est le token de début, celui qui marque le début de la séquence pour les images comme pour les textes.

Probing

Le probing (ou sondage) est une technique permettant de détecter la présence de propriétés dans un réseau de neurones. C'est une technique qui a été abondamment utilisée depuis 2018 et l'article Manning et al. qui l'applique à la détection d'arbres syntaxiques dans un transformer entraîné sur un corpus de textes étiquetés.

Ici, nous voulons utiliser le probing pour détecter la présence ou non d'une représentation du plateau de morpion, couche par couche dans le transformer. L'idée est d'entraîner un classifieur linéaire case par case et couche par couche pour qu'il détecte l'état d'une case (X, O ou vide). La technique utilisée ici est une généralisation du SVM originel, appelée OneVsRest.

Qu'est-ce qu'un SVM linéaire ?

Le SVM (Support Vector Machine) linéaire est une technique d'apprentissage supervisé utilisée pour la classification. Dans le cas binaire, l'objectif est de trouver un hyperplan qui sépare au mieux les deux classes de données. Dans le cas linéaire qui nous occupe, il s'agit donc de trouver l'hyperplan qui explique le mieux la séparation des données dans le réseau de neurones.

Soit un ensemble de données d'entraînement \(\{(x_i, y_i)\}_{i=1}^n\), où \(x_i \in \mathbb{R}^d\) sont les vecteurs de caractéristiques et \(y_i \in \{-1, +1\}\) sont les étiquettes de classe.

L'hyperplan séparateur est défini par l'équation :

\[w^T x + b = 0\]

où \(w \in \mathbb{R}^d\) est le vecteur normal à l'hyperplan et \(b \in \mathbb{R}\) est le biais.

Problème d'optimisation

Le SVM cherche à maximiser la marge entre l'hyperplan et les points les plus proches de chaque classe. Cela se traduit par le problème d'optimisation suivant :

\[ \begin{aligned} \min_{w,b} &\quad \frac{1}{2} \|w\|^2 \\ \text{s.c.} &\quad y_i(w^T x_i + b) \geq 1, \quad i = 1, \ldots, n \end{aligned} \]

En utilisant les multiplicateurs de Lagrange, on obtient la formulation duale :

\[ \begin{aligned} \max_{\alpha} &\quad \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.c.} &\quad \sum_{i=1}^n \alpha_i y_i = 0 \\ &\quad 0 \leq \alpha_i \leq C, \quad i = 1, \ldots, n \end{aligned} \]

où \(\alpha_i\) sont les multiplicateurs de Lagrange et C est un paramètre de régularisation.

Une fois les \(\alpha_i\) optimaux trouvés, la fonction de décision pour un nouveau point x est :

\[f(x) = \text{sign}\left(\sum_{i=1}^n \alpha_i y_i x_i^T x + b\right)\]

où b est calculé en utilisant les vecteurs de support (points pour lesquels \(\alpha_i > 0\)).

Extension multi-classe

Dans notre code, une approche One-vs-Rest est utilisée pour étendre le SVM binaire au cas multi-classe. Pour K classes, on entraîne K classifieurs binaires, chacun séparant une classe de toutes les autres.

Les résultats couche par couche

Le transformer est une architecture assez complexe qui permet de multiples points de sonde. Nous avons donc voulu sonder les moindres recoins de celui-ci pour avoir une idée de la représentation du plateau de morpion à chaque étape.

Voici les résultats en prenant la précision de l'évaluation du SVM couche par couche pour le texte.

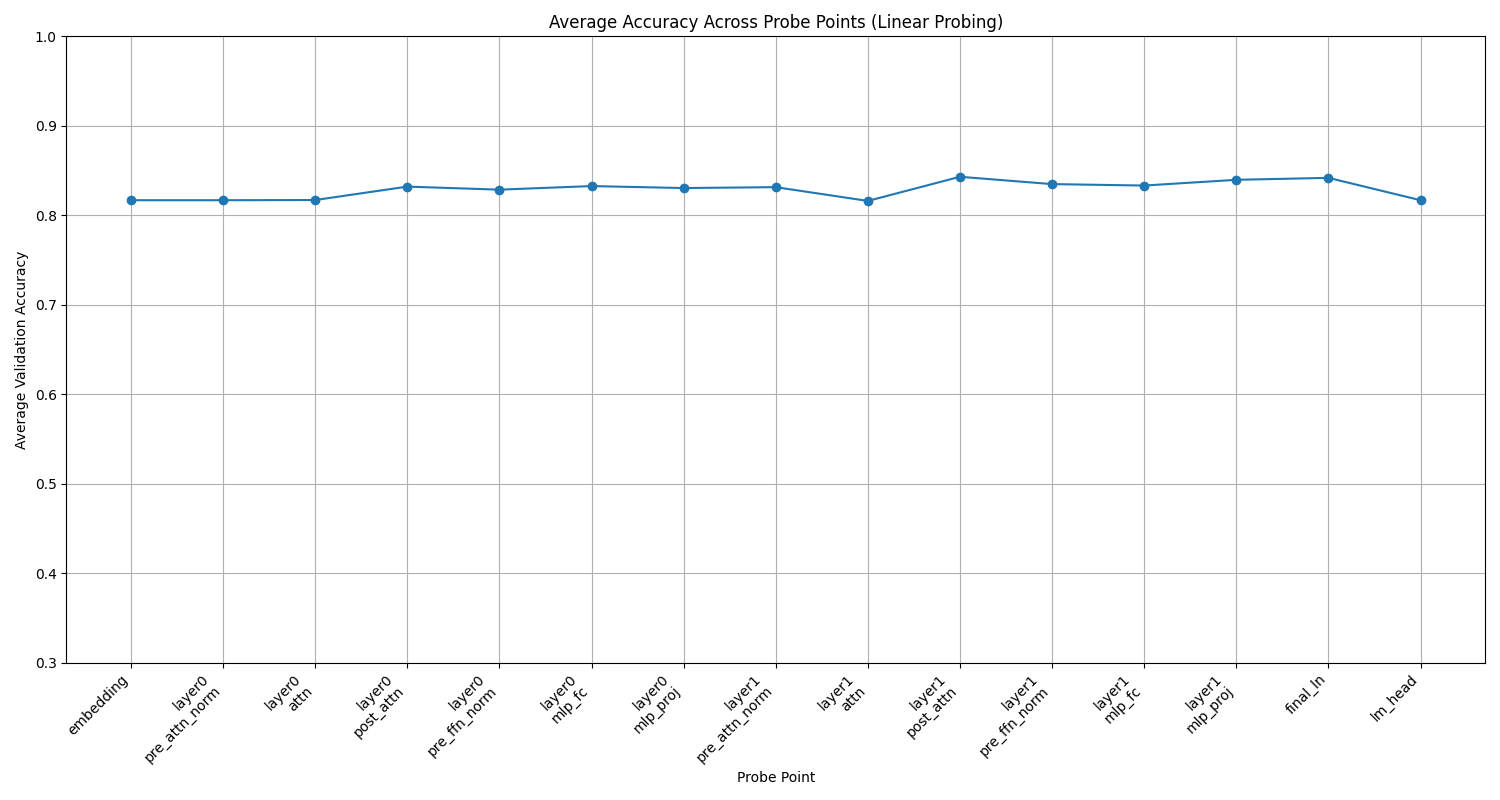
Nous pouvons observer que le transformer acquiert petit à petit une représentation de l'état du plateau de morpion, qui culmine lors de la normalisation post-attention et de la seconde couche du MLP.

Pour le modèle entraîné sur les images, le résultat est très différent, puisque la courbe reste quasiment plate tout du long du transformer.

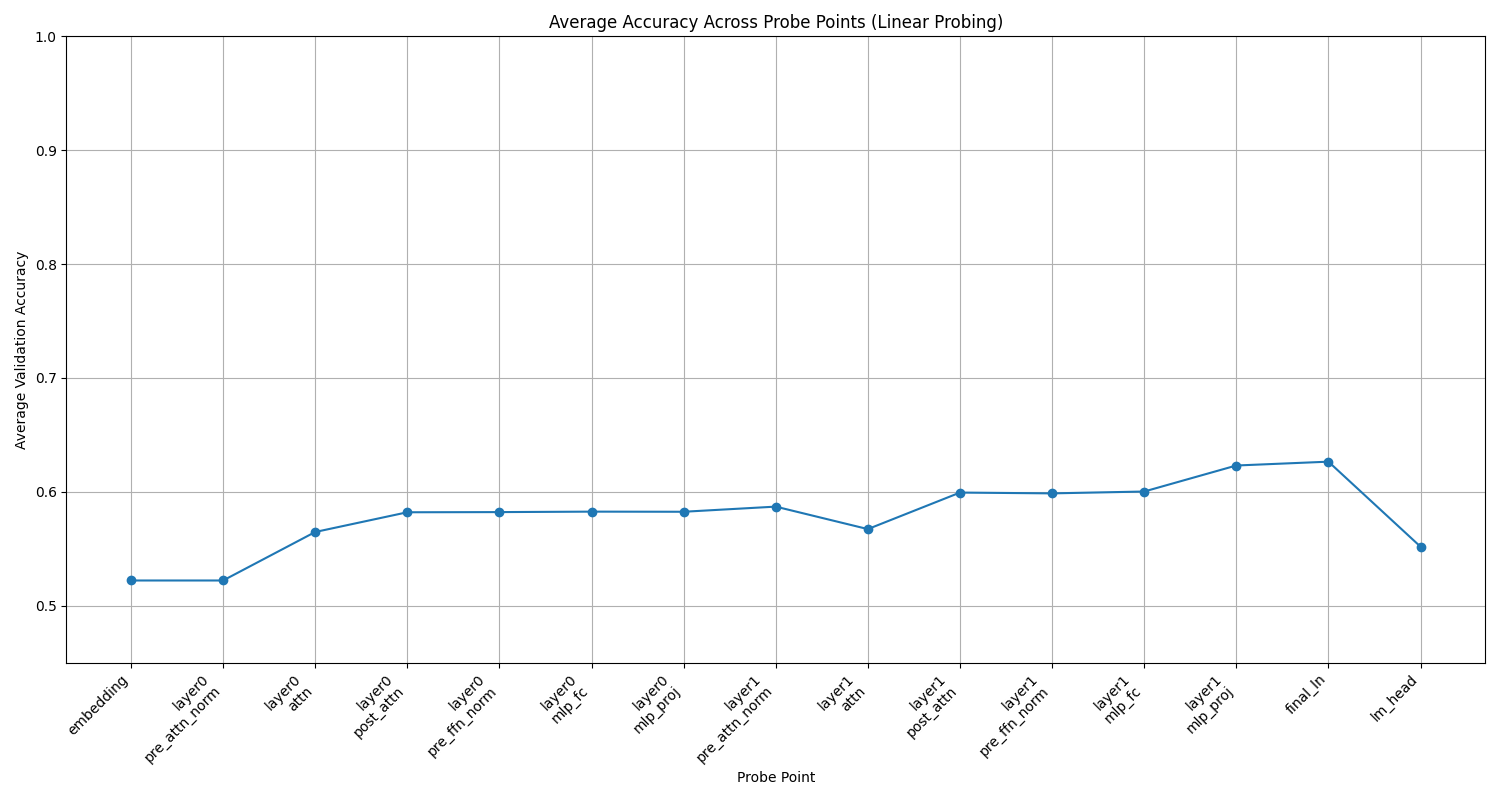
On remarque que le modèle ne forge pas de représentation du plateau de Morpion, ce qui peut interroger. Pour répondre à cela, nous pouvons formuler l'hypothèse qu'étant donné que pour résoudre la tâche (prédire le prochain token), il faut avoir une représentation sur laquelle se reposer à au moins un moment, il n'y a pas besoin de se forger une représentation lorsqu'on a déjà l'image en entrée, alors que c'est nécessaire lorsqu'on n'a que le texte.

Nous pouvons également nous intéresser à la représentation des cases (positions), qui montre des effets de symétrie et d'asymétrie assez intéressants.

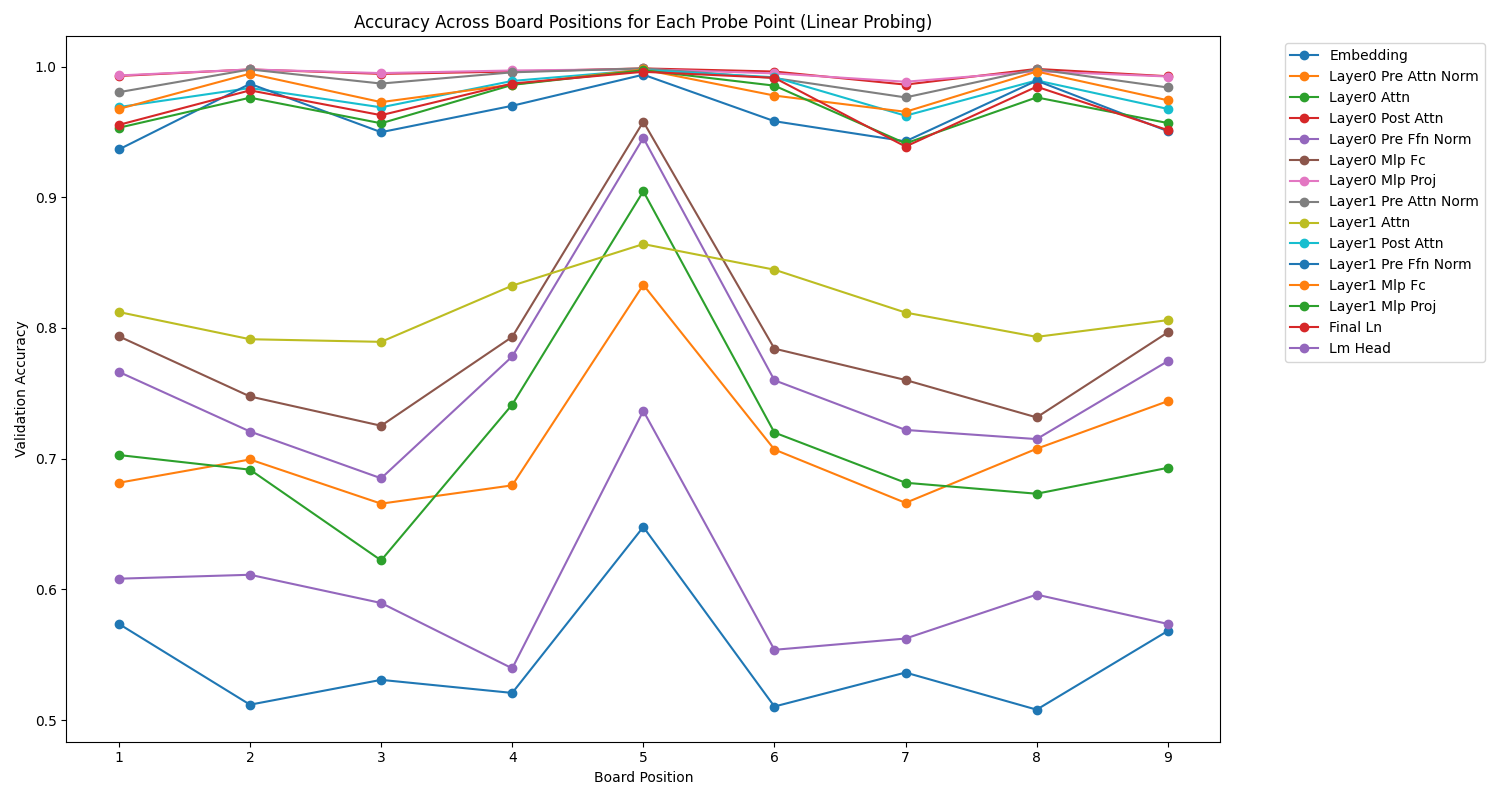
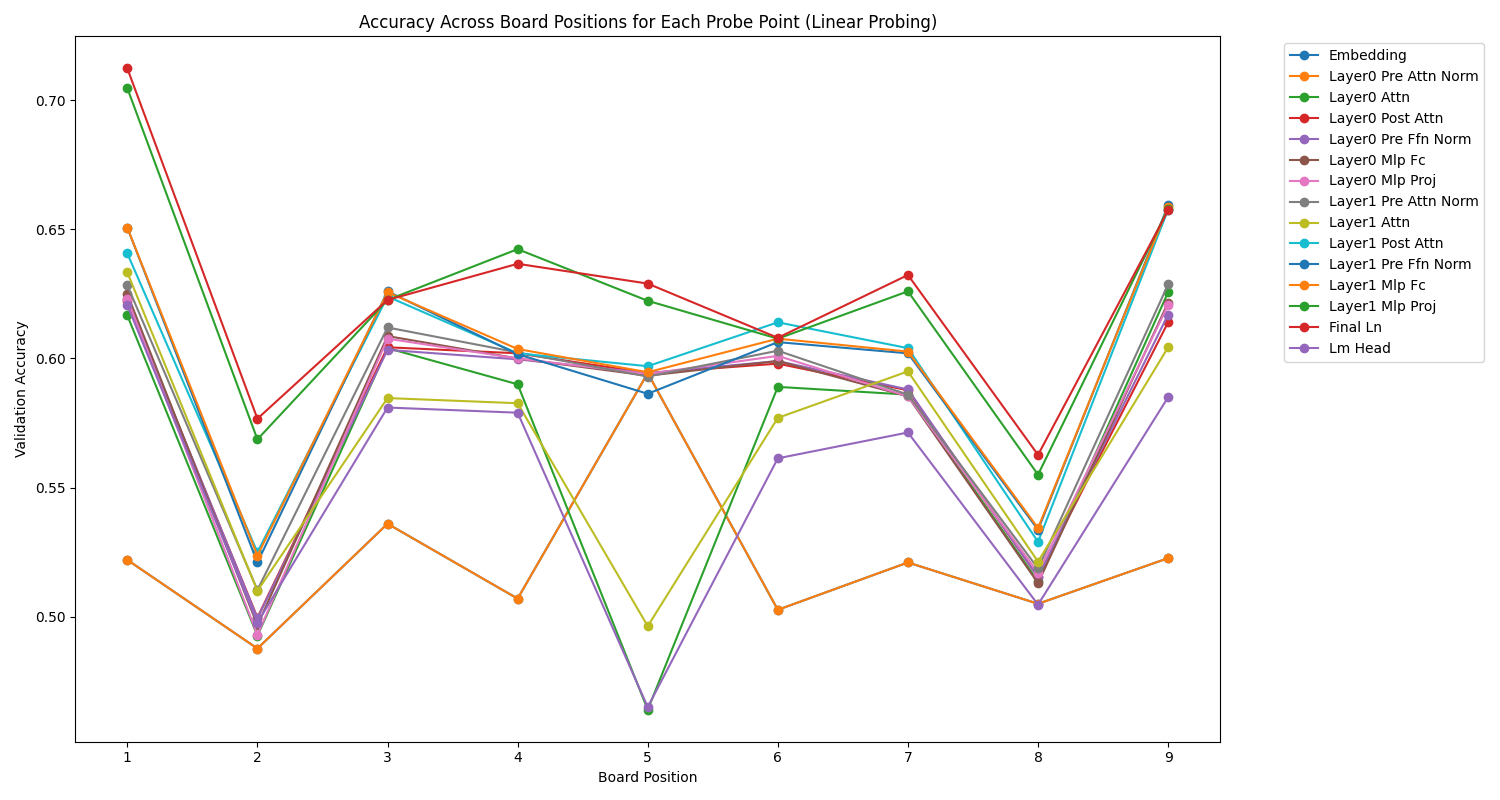
Une observation générale est que très souvent, dans la plupart des couches des deux modèles, c'est la case du milieu (position 5) qui est la mieux représentée.

Ensuite, nous pouvons observer de belles symétries, surtout pour le texte, et certaines couches, qui montrent une représentation géométrique du plateau, qui évolue en fonction de la couche. Par exemple, dans le modèle d'image, la couche de normalisation pré-attention avantage clairement la case centrale, tandis que plus on s'approche de la sortie, moins cette case du milieu est favorisée, au profit d'autres cases, comme si l'analyse effectuait un mouvement concentrique vers les bords du plateau.

La PRH se vérifie-t-elle ?

Quelles métriques ?

Suivant la littérature antérieure, nous définissons l'alignement représentationnel comme une mesure de la similarité des structures de similarité induites par deux représentations, c'est-à-dire une métrique de similarité sur les noyaux. Nous donnons la définition mathématique de ces concepts ci-dessous :

• Une représentation est une fonction f : X → ℝ^n qui attribue un vecteur de caractéristiques à chaque entrée dans un certain domaine de données X.
• Un noyau, K : X × X → ℝ, caractérise comment une représentation mesure la distance/similarité entre les points de données. K(x_i,x_j)=⟨f(x_i),f(x_j)⟩, où ⟨·,·⟩ désigne le produit scalaire, x_i,x_j ∈ X et K ∈ 𝒦.
• Une métrique d'alignement de noyau, m : 𝒦 × 𝒦 → ℝ, mesure la similarité entre deux noyaux, c'est-à-dire à quel point la mesure de distance induite par une représentation est similaire à celle induite par une autre. Les exemples incluent la Distance de Noyau Centrée (CKA), SVCCA, et les métriques des plus proches voisins.

Métriques d'alignement

Cycle KNN (K plus proches voisins cycliques)

Définition mathématique
Soient A et B deux ensembles de vecteurs de caractéristiques, chacun de taille N. Pour un k donné :

1. Calculer les k-NN dans A : Pour chaque point dans A, trouver ses k plus proches voisins dans A.
2. Mapper ces voisins vers B.
3. Calculer les k-NN dans B pour ces points mappés.
4. Vérifier si le point original dans A est parmi ces voisins.

La métrique est la fraction de points qui "survivent" à ce cycle.

Formule

\[ \text{Cycle\_KNN}(A, B) = \frac{1}{N} \sum_{i=1}^N \mathbb{I}(a_i \in \text{kNN}_B(\text{kNN}_A(a_i))) \]

où \(\mathbb{I}\) est la fonction indicatrice, et \(\text{kNN}_X(y)\) renvoie les k plus proches voisins de y dans X.

Interprétation

• Plage : [0, 1]
• Des valeurs plus élevées indiquent un meilleur alignement entre les deux espaces de caractéristiques.
• Une valeur de 1 signifie une parfaite consistance cyclique : la structure de voisinage est parfaitement préservée lors du mapping de A vers B et retour.
• Des valeurs plus basses suggèrent que la structure locale n'est pas bien préservée entre les deux espaces.

KNN mutuel (K plus proches voisins mutuels)

Définition mathématique
Pour chaque point dans A, vérifier s'il est parmi les k-plus proches voisins de son point correspondant dans B, et vice versa.

Formule

\[ \text{Mutual\_KNN}(A, B) = \frac{1}{N} \sum_{i=1}^N \mathbb{I}(a_i \in \text{kNN}_B(b_i) \text{ ET } b_i \in \text{kNN}_A(a_i)) \]

où \(\mathbb{I}\) est la fonction indicatrice, et \(\text{kNN}_X(y)\) renvoie les k plus proches voisins de y dans X.

Interprétation

• Plage : [0, 1]
• Des valeurs plus élevées indiquent une meilleure préservation mutuelle du voisinage entre les deux espaces.
• Une valeur de 1 signifie que tous les points sont des k-plus proches voisins mutuels dans les deux espaces.
• Des valeurs plus basses suggèrent que les structures de voisinage dans A et B sont différentes.

CKA (Alignement de Noyau Centré)

Définition mathématique
CKA mesure la similarité entre deux noyaux après centrage.

Formule

\[ \text{CKA}(K, L) = \frac{\langle K_c, L_c \rangle_F}{\|K_c\|_F \|L_c\|_F} \]

où \(K_c\) et \(L_c\) sont des matrices de noyau centrées, \(\langle \cdot,\cdot \rangle_F\) est le produit scalaire de Frobenius, et \(\|\cdot\|_F\) est la norme de Frobenius.

Interprétation

• Plage : [0, 1]
• Des valeurs plus élevées indiquent une plus grande similarité entre les matrices de noyau.
• Une valeur de 1 suggère que les deux noyaux capturent des relations identiques entre les points de données.
• Des valeurs plus basses indiquent que les noyaux capturent des relations différentes.
• CKA est invariant aux transformations orthogonales et à la mise à l'échelle isotrope.

SVCCA (Analyse de Corrélation Canonique des Vecteurs Singuliers)

Définition mathématique

1. Effectuer la SVD sur les deux matrices de caractéristiques : A = U_A Σ_A V_A^T, B = U_B Σ_B V_B^T
2. Prendre les d premiers vecteurs singuliers : Ũ_A, Ũ_B
3. Effectuer la CCA sur ces matrices tronquées

Formule

\[ \text{SVCCA}(A, B) = \frac{1}{d} \sum_{i=1}^d \rho_i \]

où \(\rho_i\) sont les corrélations canoniques entre \(\tilde{U}_A\) et \(\tilde{U}_B\).

Les étapes pour calculer SVCCA sont :

1. Effectuer la SVD sur les deux matrices de caractéristiques : \[A = U_A \Sigma_A V_A^T, \quad B = U_B \Sigma_B V_B^T\]
2. Prendre les d premiers vecteurs singuliers : \(\tilde{U}_A, \tilde{U}_B\)
3. Effectuer la CCA sur ces matrices tronquées

Interprétation

• Plage : [0, 1]
• Des valeurs plus élevées indiquent une corrélation plus forte entre les composantes principales des deux espaces de caractéristiques.
• Une valeur proche de 1 suggère que les principales directions de variation dans les deux espaces sont fortement alignées.
• Des valeurs plus basses indiquent que les composantes principales des deux espaces capturent différents aspects des données.
• SVCCA est moins sensible au bruit comparé à la simple CCA, en raison de l'étape initiale de SVD.

Conclusion

Ces métriques fournissent différentes perspectives sur l'alignement entre deux ensembles de caractéristiques :

• Cycle KNN et Mutual KNN sont plus sensibles aux structures locales et peuvent être utiles pour détecter des alignements fins.
• CKA est plus robuste et capture des similarités globales, mais peut manquer des détails fins.
• SVCCA est utile pour comparer les principales directions de variation, mais peut ignorer les caractéristiques moins importantes.

En pratique, il est souvent bénéfique d'utiliser plusieurs de ces métriques ensemble pour obtenir une image plus complète de l'alignement entre deux ensembles de caractéristiques.

Les résultats

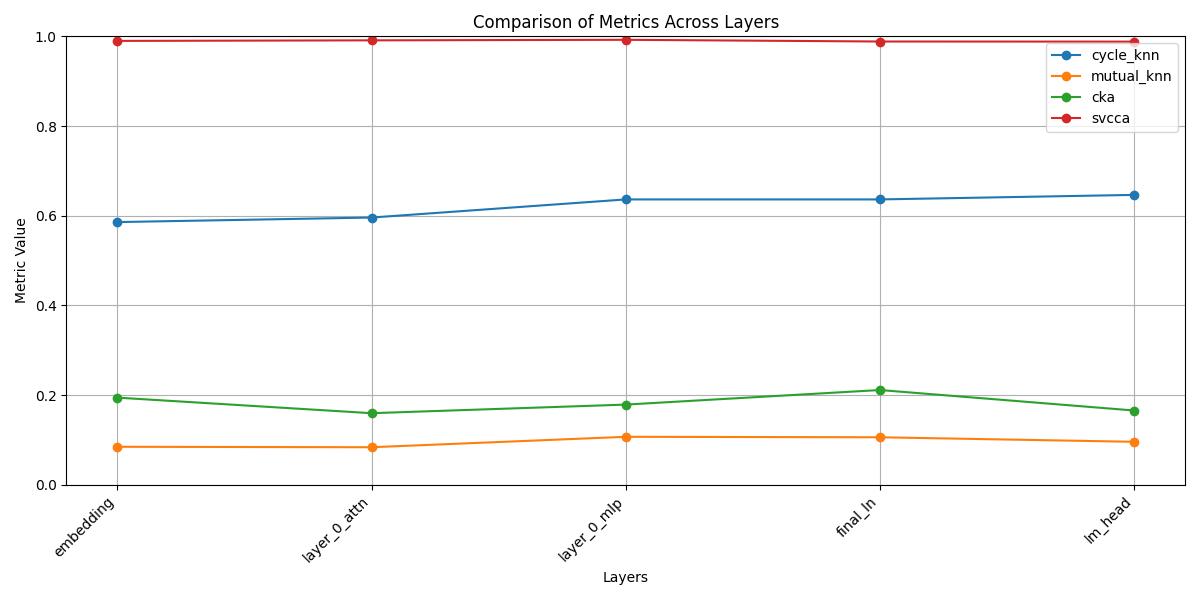
Bibliographie

1. Huh, M., Cheung, B., Wang, T., & Isola, P. (2024). The Platonic Representation Hypothesis. arXiv preprint.
2. Kornblith, S., Norouzi, M., Lee, H., & Hinton, G. (2019). Similarity of neural network representations revisited. In International Conference on Machine Learning (pp. 3519-3529). PMLR.
3. Raghu, M., Gilmer, J., Yosinski, J., & Sohl-Dickstein, J. (2017). SVCCA: Singular vector canonical correlation analysis for deep learning dynamics and interpretability. In Advances in Neural Information Processing Systems (pp. 6076-6085).
4. Karvonen, A. (2024). Emergent World Models and Latent Variable Estimation in Chess-Playing Language Models. arXiv preprint.